John Greschak - Learning OZ Pitch Names

Learning OZ Pitch Names

by John Greschak

January 23, 2003

Introduction
Simple Mnemonic Devices
Twelve Poems for Recognizing Intervals
Animated GIFs for Instruments
Update History

Introduction

In this article, various techniques are described that may be used to learn the pitch names associated with the OZ pitch-naming convention. For a definition of the OZ pitch-naming convention, see: The OZ Pitch-Naming Convention.

Simple Mnemonic Devices

There are some simple mnemonic devices that one might use to remember various properties of OZ pitch names. Here is a list of some such devices:

The Wizard of OZ: The first pitch-class name letter is O. The last is Z.
Origin: The basis of both octaves and the pitch-class name sequence is O, which is the first letter of the word origin.
Oh: The pitch name of (roughly) 1 Hz is the word Oh.
Zn: The name of the highest pitch in the octave that contains the highest frequency that humans can hear is Zn, the chemical symbol for zinc.
MOI: There is no "MOI" (the French word for "me") in OZ. The letters M, O and I are the only letters that are not used for octave names.
Man Octaves: The place were M would have occurred in the sequence of octave letters (had it been used) is replaced by the numerals 0 through 9. This band of octaves may be thought of as the middle octaves or man octaves because these are the octaves that are (for the most part) between the infrasonic and ultrasonic frequency ranges and these are the frequencies that can be heard by man.

Twelve Poems for Recognizing Intervals

Here, number words shall be used for interval names. The relationship between numeric interval names and traditional interval names is given in the following table:

Interval Names
Numeric Interval Name	Traditional Interval Name
Zero	Unison
One	Minor Second
Two	Major Second
Three	Minor Third
Four	Major Third
Five	Perfect Fourth
Six	Tritone
Seven	Perfect Fifth
Eight	Minor Sixth
Nine	Major Sixth
Ten	Minor Seventh
Eleven	Major Seventh

In the article Twelve Circular Poems on the Letters O through Z, twelve poems are presented, each of which is associated with one of the twelve possible interval sizes that might exist between two pitches that are less than one octave apart. These poems may be used to identify the intervallic relationship between two pitches.

For example, suppose one is to identify the melodic interval between the sequence of pitches Q5 and V4. To determine that this interval is a seven down, one could (mentally) proceed through the following steps:

Recognize that the pitch V4 is lower than the pitch Q5, and consequently the ordered pair of letters to be used for interval identification is VQ (rather than QV).
Recall that the word VanQuish is associated with the ordered pair of letters VQ.
Recall that the word VanQuish is used in the poem Dodecagon of Sevens, and therefore, the interval from the pitch Q5 down to the pitch V4 must be a seven.

We may consider these three steps independently.

Recognizing the Lower Pitch of a Pair of Pitches

This first step in the process is relatively easy in the case when the octave names for the pitches are numbers and the octave numbers of the two pitches are different. In this case, the pitch with the lower octave number must be the lower pitch (e.g. V4 must be lower than Q5). However, this step is somewhat more difficult to complete when the octave names of the two pitches are identical. Then, one must use the natural ordering of the letters of the alphabet to determine which pitch is lower. For example, in order to recognize that the pitch Q4 is lower than V4, one must know that Q comes before V in the alphabet.

For pitch-name pairs (with the same octave name) that involve the pitch-class names O or Z, it is easy to determine which pitch is lower (as in O4 V4 or V4 Z4). That with the pitch-class name O will be the lower. That with the pitch-class name Z will be the higher. More generally, it might help one to think of the sequence O P Q R S T U V W X Y Z as being composed of the following two subsequences: O P Q R S T and U V W X Y Z. Generally, pitches for which the pitch-class name is O, P, Q, R, S or T (U, V, W, X, Y or Z) will be the lower (higher) pitch. The exceptions occur when both pitches are in the same subsequence (as in P4 R4). For this, one must know the ordering of each subsequence very well.

To make it easier for one to identify the lower pitch of a pair of pitches, one might use the characters / and \ between pitch names of a sequence. For example, consider the following sequence of pitches: U4 V3 O4 T3 S3 V3. This sequence might be notated as.

U4\V3/O4\T3\S3/V3

Here, the character \ between U4 and V3 indicates that V3 is lower than U4. The character / between V3 and O4 indicates that O4 is higher than V3 (or equivalently, V3 is lower than O4).

Alternatively, pitch names might be displaced graphically to indicate relative pitch levels. For this purpose, pitch levels might be represented either horizontally or vertically.

For example, one might represent pitch levels vertically as:

                         Z4
   --------------------Y4-----
                     X4
   ----------------W4---------
                 V4
   ------------U4-------------
             T4
   --------S4-----------------
         R4
   ----Q4---------------------
     P4
   O4=========================
                         Z3
   --------------------Y3-----
                     X3
   ----------------W3---------
                 V3
   ------------U3-------------
             T3
   --------S3-----------------
         R3
   ----Q3---------------------
     P3
   O3=========================

Using this convention, one might notate the sequence of pitches considered here as:

---------------------------

U4-------------------------

---------------------------

====O4=====================

---------------------------

   ---------------------------
     V3      V3
   ---------------------------
         T3
   --------S3-----------------

---------------------------

===========================

Or, more simply, as:

---------------------------

U--------------------------

---------------------------

4----O----------------------

---------------------------

    ---------------------------
      V       V
    ---------------------------
          T
    --------S------------------

---------------------------

A horizontal displacement of pitches might be particularly useful for keyboard instruments such as the piano. With this notation, time would advance (uniformly) from top to bottom. For example, the sequence of pitches being considered here might be notated as:

   2|||||||||||3|||||||||||4|||||||||||5|||||||||||6|||||||||||7
                                 U
                      V
                           O
                    T
                   S
                      V

Recalling the Word Associated with a Given Ordered Pair of Letters

The following word matrix gives the 144 words that are used in the Twelve Circular Poems on the Letters O through Z:

O P Q R S T U V W X Y Z

O OOps OPus OQuassa O-Ring OSaka One-Track OUch OVer OWl OXen OY OZone

P POle Ping-Pong PiQuant PaRent PostScript Part-Time PUsh PolyVinyl PoWer PiXie PinYin PizZa

Q QuestiOn QuakeProof QuinQuennial QueRy QuickSand QuieT QUebec QuiVer QWerty QuiXotic QuaYage QuiZ

R ROdeo RaP ReQuiem RailRaod ReSet RaTed ReUse RiVer RailWay RX RoYal RaZz

S SO SPy SeQuel SiRen SeeSaw STate SUnday SaVing SouthWest SiX SaY SiZe

T TO TeePee TorQue TeaRoom TailSpin Tête-à-Tête TenUous TV ToWer TeXas TYing TimeZone

U Uh-Oh UP UniQue URban US U-Turn UlUlate UV UnWed UXorial UnYielding UnZip

V VOcal ViPer VanQuish ViceRoy VerSus VaTican VolUme Vis-à-Vis VieWing ViXen VoYage VeneZuela

W WalkOut WordPlay WaitQueue WeaRy WaS WaTer Wake-Up WaVe WorldWide WaXy WhY WiZard

X XOr eXPert eXQuisite X-Ray eXceSs eXTend eXUdate eXcaVate XWay eX-eX XY-plane eX-Zebra

Y YellOw YipPee YQ Year-Round YeS YeTi YUkon YaVapai YaWn Y-aXis Yo-Yo YaZoo

Z ZOo ZapPer Zero-Quantum ZurRich ZeptoSecond ZiTi ZaiUs ZanesVille ZimbabWe ZaX ZYgote ZigZag

This table may be used to learn the particular word that is associated with each possible ordered pair of pitch-class names. For example, the word that is associated with the order pair UT, is U-Turn, which is located in row U of column T in the table.

The color used for a particular cell of this table matches the color used for the poem with which the word in the cell is associated. For example, the color of the cell that contains the word X-Ray is red. This matches the color that is shown to the left and right of the poem Line Segments of Sixes on the page Twelve Circular Poems on the Letters O through Z.

Recalling the Poem in which a Given Word is Used

In order to perform this step rapidly, one might memorize all twelve poems (as well as their titles). In addition to memorizing the sequence of words in each poem, one could memorize a complex of associations such as the associated melodic intervals, the associated polygonal shapes, the geometric positions of each word within those shapes, and the color that is associated with each poem. By using a variety of verbal, visual and aural relationships such as this, one could strongly bond a particular word to a particular poem.

For example, to recall that the word UnYielding is used in the poem Triangles of Fours, one might recall any of the following relationships:

The word UnYielding is part of the phrase "UnYielding YQ", which occurs in the poem.
The word UnYielding is sung using the interval four.
The word UnYielding occurs at the bottom right corner of a triangle in one of the poems.
The word UnYielding occurs in the yellow poem.

When one has memorized a complex of relationships such as this, it is easy to recall that the word UnYielding is used in the poem Triangles of Fours.

Word Phrases

To recall a phrase of which a given word is a component, it helps to know that throughout the twelve poems, the word that follows a given word, always begins with the second bold-faced letter of the word that it follows. For example, YQ follows UnYielding, and YQ begins with Y, which is the second bold-faced letter of UnYielding. The words that begin with eX instead of X (i.e. eX-eX, eX-Zebra, eXPerT, eXQuisite, eXceSs, eXTend, eXUdate and eXcaVaTe) are the only exceptions to this pattern.

Further, some words contain more than two bold letters. For example, consider the word PoWeR in the poem Dodecagon of Sevens. The second and third bold letters of a word such as this will be the first and second bold letters of the next word in the sequence. For example, the word WeaRY follows PoWeR. The second and third bold letters of PoWeR (i.e. W and R) are the first and second bold letters of WeaRY. Similarly, the second and third bold letters of WeaRY are the first and second bold letters of RoYal, which is the word that follows WeaRY.

When memorizing, one might visualize the first pair of bold-faced letters of each word as the word is spoken (either aloud or silently).

Melodic Intervals

Rather than speaking a poem, one might sing each word (either aloud or silently) using a sequence of two pitches that are separated by the interval that is associated with the word. For example, each word of the poem Dodecagon of Sevens could be sung using the pitches O3 and V3 (or O4 and V4, depending upon one's vocal range). For the word OVer (pronounced "oh-ver"), the syllable "oh" could be sung at the pitch O3 while the syllable "ver" could be sung at the pitch V3. The next word VanQuish could be sung using the same pair of pitches (O3 and V3). Alternatively, suitable V and Q pitches could be used (e.g. V3 and Q4, or V2 and Q3, again depending upon one's range).

Geometric Shapes

There is a shape associated with each poem and interval size. The interval name that is associated with a given poem dictates the shape for the poem. For example, Triangles of Fours consists of triangular cycles because 12 divided by 4 (i.e. the interval name) equals 3. Similarly, Line Segments of Sixes consists of line segments (or pairs of points) because 12 divided by 6 is 2. Conversely, the intervals that are associated with a given geometric shape may be determined by dividing 12 by the number of vertices in the shape. For example, to determine the intervals associated with a square, one could divide 12 by 4 (i.e. the number of vertices in a square) to obtain 3. Three is one of the intervals associated with a square. The other interval is the complement of 3, which is 9. The complete list of intervals that are associated with each of the possible geometric shapes is given in the following table:

Geometric Shape Interval(s)

Point 0

Line Segment 6

Triangle 4 and 8

Square 3 and 9

Hexagon 2 and 10

Dodecagon 1 and 11, and
7 and 5

Colors

A color has been assigned to each poem and its corresponding interval. Colors are shown to the left and right of each poem on the page Twelve Circular Poems on the Letters O through Z. First, a color was assigned to each of the following musical intervals: zero, one, two, three, four, six and seven. Then, pale versions of these colors were assigned intervals that are the complement of one of these intervals. For example, a two is orange while a ten is pale orange. The following table lists mnemonic devices that may be used to remember the color that is associated with a particular interval:

Colors for Intervals

Sevens are Green.
Green represents "go". A seven is a "go" interval because it is consonant. Traditionally, it is an interval that is permitted to continue in time. Also, green is generally thought to be a restful color, and consonance is restful. Fives are Pale Green.

Sixes are Red.
Red represents "stop". A six is a "stop" interval because it is dissonant. Traditionally, it is an interval that is transient and resolved to another interval rather than permitted to continue in time.

Threes are Blue.
Threes are used in blues music. One of the so-called blue notes is the third note of the minor scale, which is a three above the first note of the scale. Nines are Pale Blue.

Zeros are Gray.
The "colorless" gray represents the harmonic properties of this interval. The interval of a zero is harmonically "colorless" because no difference tones are generated when two identical pitches are sounded.

Fours are Yellow.
Yellow (i.e. red plus green) represents the fact that this interval is both consonant (green) and dissonant (red). It is said to be an imperfect consonance. Eights are Pale Yellow.

Twos are Orange.
Orange (i.e. red plus yellow) represents that fact that this interval is dissonant though somewhat consonant. The slight degree of consonance arises from the fact that twos occur frequently in major and minor scales and they are formed by concatenating two sevens. But they are primarily dissonant. Specifically, they are more dissonant (red) that fours (yellow). Tens are Pale Orange.

Ones are Magenta.
Magenta (i.e. red plus blue) represents the fact that this interval is quite dissonant like a six (red) but at the same time suggestive of a minor key (blue) because there are two such intervals in a descending minor scale. Elevens are Pale Magenta.

Animated GIFs for Instruments

In this section, several animated GIFs are given that may be used to learn the OZ pitch names associated with various instruments. In each of these GIFs, an unadorned schematic of the instrument is shown without pitch names for approximately 2.5 seconds. Then, pitches are superimposed on the schematic and displayed for 2.5 seconds. Each GIF loops continuously between the unadorned and adorned schematics. To use these GIFs for learning purposes, one may focus attention upon a particular element of the unadorned schematic (e.g. a particular piano key, or a particular fret or position of a stringed instrument) and attempt to identify the pitch name associated with that element. Then, one may compare this name with the pitch name that is displayed in the adorned schematic.

Piano

The following animated GIF may be used to learn the OZ pitch-class name for each key on the piano:

OZ Pitch Classes for Piano

Here is a list of some mnemonic devices that one might use to remember the OZ pitch-class names for piano keys:

PRUWY: When read from left to right, the black keys spell the word "PRUWY" (pronounced "proo'-wee").
OQ and PR: When O, P, Q and R are in the same octave, Q is the two above O and R is the two above P. The second letter Q (R) in the sequence OQ (PR) is obtained from O (P) by adding a small diagonal slash to the lower right corner of the letter.
ST: The letters S and T are the pitch-class names of two adjacent white keys that are not separated by a black key. The sequence of letters ST occurs often in words.
VXZ: These are the only three keys that are not covered by the other mnemonic devices. These keys can be learned by using the phrase ViXen eX-Zebra from the poem Hexagons of Twos.

Guitar

The following animated GIF may be used to learn the OZ pitch name for each position on a six-string guitar that is tuned to the pitches S2, X2, Q3, V3, Z3 and S4:

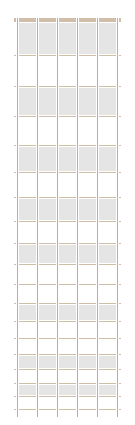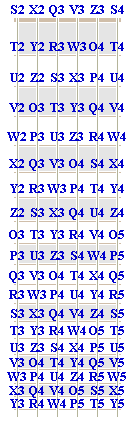
OZ Pitch Names for Guitar

For a guitar, the interval between adjacent open string pairs is a five, except for (V3, Z3) for which the interval is a four. Consequently, the poems Dodecagon of Fives and Triangles of Fours may be used to remember the sequence of pitch names across any given fret. For example, the names of the pitches across the sixth fret are Y2, R3, W3, P4, T4 and Y4. The associated sequence of pitch-class names (i.e. Y, R, W, P, T and Y) may be remembered by using the following three phrases: Year-Round RailWay WordPlay from the poem Dodecagon of Fives, Part-Time from the poem Triangles of Fours, and TYing from the poem Dodecagon of Fives.

Violin

The following animated GIF may be used to learn the OZ pitch name for each position on a violin:

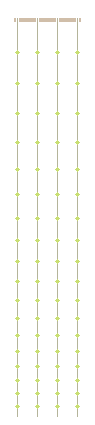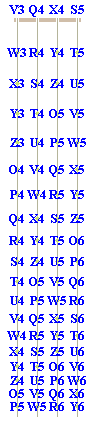
OZ Pitch Names for Violin

For a violin, the interval between adjacent open string pairs is a seven. Consequently, the poem Dodecagon of Sevens may be used to remember the sequence of pitch names across any given position. For example, the names of the pitches that would ordinarily be played by the first finger in the sixth position are P4, W4, R5 and Y5. The associated sequence of pitch-class names (i.e. P, W, R and Y) may be remembered by using the following phrase: PoWeR WeaRy RoYal from the poem Dodecagon of Sevens.

Note: In the same way, the poem Dodecagon of Sevens may be used to remember the pitch-name sequences across any given position of a viola or cello (because the interval between adjacent open string pairs on these instruments is seven as well).

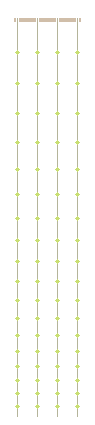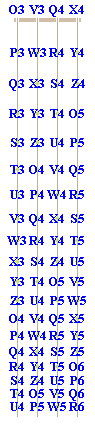
Viola

The following animated GIF may be used to learn the OZ pitch name for each position on a viola:

OZ Pitch Names for Viola

Cello

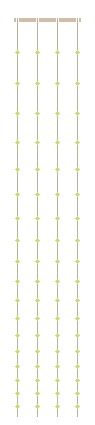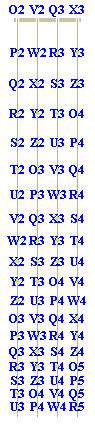
The following animated GIF may be used to learn the OZ pitch name for each position on a cello:

OZ Pitch Names for Cello

Double Bass

The following animated GIF may be used to learn the OZ pitch name for each position on a double bass:

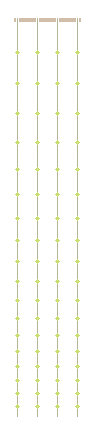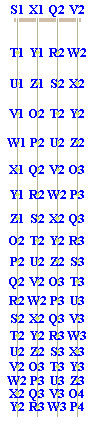
OZ Pitch Names for Double Bass

For a double bass, the interval between adjacent open string pairs is a five. Consequently, the poem Dodecagon of Fives may be used to remember the sequence of pitch names across any given position. For example, the names of the pitches that would ordinarily be played by the first finger in the sixth position are Y1, R2, W2 and P3. The associated sequence of pitch-class names (i.e. Y, R, W and P) may be remembered by using the following phrase: Year-Round RailWay WordPlay from the poem Dodecagon of Fives.

Update History

January 23, 2003: Completed the first version of this page.

Geometric Shape	Interval(s)
Point	0
Line Segment	6
Triangle	4 and 8
Square	3 and 9
Hexagon	2 and 10
Dodecagon	1 and 11, and 7 and 5

Colors for Intervals
Sevens are Green. Green represents "go". A seven is a "go" interval because it is consonant. Traditionally, it is an interval that is permitted to continue in time. Also, green is generally thought to be a restful color, and consonance is restful.	Fives are Pale Green.
Sixes are Red. Red represents "stop". A six is a "stop" interval because it is dissonant. Traditionally, it is an interval that is transient and resolved to another interval rather than permitted to continue in time.
Threes are Blue. Threes are used in blues music. One of the so-called blue notes is the third note of the minor scale, which is a three above the first note of the scale.	Nines are Pale Blue.
Zeros are Gray. The "colorless" gray represents the harmonic properties of this interval. The interval of a zero is harmonically "colorless" because no difference tones are generated when two identical pitches are sounded.
Fours are Yellow. Yellow (i.e. red plus green) represents the fact that this interval is both consonant (green) and dissonant (red). It is said to be an imperfect consonance.	Eights are Pale Yellow.
Twos are Orange. Orange (i.e. red plus yellow) represents that fact that this interval is dissonant though somewhat consonant. The slight degree of consonance arises from the fact that twos occur frequently in major and minor scales and they are formed by concatenating two sevens. But they are primarily dissonant. Specifically, they are more dissonant (red) that fours (yellow).	Tens are Pale Orange.
Ones are Magenta. Magenta (i.e. red plus blue) represents the fact that this interval is quite dissonant like a six (red) but at the same time suggestive of a minor key (blue) because there are two such intervals in a descending minor scale.	Elevens are Pale Magenta.